脉冲神经网络的无监督学习规则

发表于 分类于 阅读次数： Valine：

人工神经网络的无监督学习

输入的是无标签数据，没有用来指导突触权值修改过程的实际输出和期望输出之间的误差或者奖励信号。

神经网络通过一些学习算法自动调整网格参数，一般分为两种算法：

  1. 全局学习算法，参照全局视图来修改突触；
  2. 局部学习算法，每一个神经元自己通过算法根据输入输出来修改权值。

脉冲神经网络的无监督学习是一种具有生物可解释性的学习规则，在机器学习中占用重要的地位。

突触可塑性机制是生物神经系统学习和记忆的基础。

Hebb规则指出：两个神经元之间的突触连接强度随着两个神经元状态的变化而变化，并且只与这两个神经元有关。

而脉冲时间可塑性机制stdp是Hebb规则的扩展。

突触可塑性机制

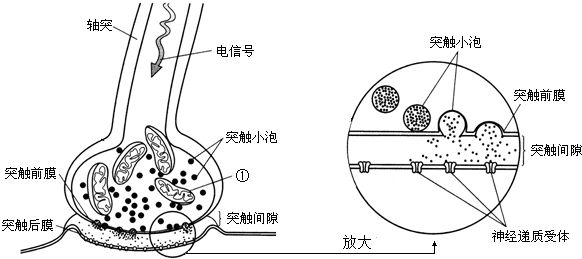
突触相关基本概念：

  • 突触：神经元之间相互连接，实现信息传递的部分。

  • 突触前神经元：传出信息的神经元。

  • 突触后神经元：接收信息的神经元。

  • 突触后电位：突触前神经元的脉冲传入突触后，使得突触后神经元的膜电位发生改变。

  • 突触具有兴奋性和抑制性两种类型。

突触可塑性机制定义：

在体内外各种因素的影响下不断变化、更新和重塑，以适应机体功能。

分类

  • 短时程
  • 长时程
    • 长时程增强（long-term potentiation,LTP）
    • 长时程抑制（long-term depression,LTD）

突触长时程增强LTP

是发生在两个神经元信号传输中的一种持久的增强现象，能够同步的刺激两个神经元。

突触长时程抑制LTD

与突触长时程相反，表示突触传递效率长时程降低。

Hebb学习规则

该规则给出的突触可塑性假设为：如果神经元A的轴突与神经元B足够接近，并能反复或持续地刺激神经元B并使之发放脉冲，神经元A的轴突到神经元B的突触效能就会增强。

Hebb学习规则的数学模型

  1. 一般性框架

    神经元j的活动可以通过他发放的频率$v_j$来描述，发放频率可以表示为神经元膜电位$u_j$的函数：

    $g$为非线性单调递增函数；

    突触后神经元$j$的膜电位可以通过突触前神经元$i$的发放频率$vi$和$w{ij}$来计算

    Hebb学习规则满足局部特性，权值$w_{ij}$只依赖于突触前后的两个神经元。

    神经元的膜电位也可以根据上面的式子来计算$u_j=g^{-1}(v_j)$，其中$g^{-1}$表示$g$反函数的。

    频率模型中突触变化仅与本地突触权值$w_{ij}$相关，因此突触权值的改变量为：

    使用泰勒公式展开可得：

  2. 变化形式

    设置以上泰勒公式的各个常数为不同的值，可得到学习规则的不同变化形式。

  3. 突触增强或者抑制的方式

    原始Hebb规则并没有给出减小突触权值的方式，仅给出了增强的参考条件。

    所以我们需要考虑突触抑制机制。

Hebb学习规则相关性质

  1. 有界性

    兴奋性突触的权值应处于一个有界的范围$[0,w_{max}]$

  2. 竞争性

    一些权值增大的时候，其他权值必须减少。

  3. 稳定性

    虽然学习阶段结束，突触权值被认为是固定的参数，但是神经系统通过处理不同的输入，系统要保持一定的适应性，且之前学习到的信息不能丢失。

STDP学习规则

Hebb学习规则根据神经元脉冲发放的频率进行突触权值的更新。

而实际上，突触前和突触后脉冲发放相对时间差对神经元之间的突触的改变方向和大小具有关键作用。

STDP学习规则的数学模型

突触权值的变化是一个关于时间的分段函数，突触的变化值取决于突触前后脉冲的相对时间。

  1. STDP学习规则的一般形式

    设：突触前神经元i

    突触后神经元j

    两者之间连接的神经上的权值为$w_{ij}$

    则有STDP学习机制为：

    • 如果在突触前神经元i 发放的脉冲到达突触之后，突触后神经元j才响应并发放脉冲，则权值$w_{ij}$增加
    • 如果在突触后神经元j发放脉冲后，突触前神经元i才传递脉冲，那么这个信息可能被忽略，权值$w_{ij}$会减弱

    ps：存在与以上机制相反的突触变化过程，称为anti-STDP学习机制。

  2. STDP学习规则学习窗口

    待更新

  1. 突触权值的学习过程分析

    主要分为四种情况：

    • 如图(a)，当突触前和突触后神经元都不发放脉冲时，零阶项$a0<0$将引起突触权值$w{ij}$
    • 如图(b)，当突触前脉冲到达或突触后脉冲发放时，线性阶项会改变突触权值。当$a1^{pre}>0$时，当突触前脉冲在$t_i^f$时到达，引起权值$w{ij}$增加；当$a1^{post}<0$时，每一个突触后脉冲在$t_j^f$时到达，引起权值$w{ij}$减小。
    • 如图(c)，假设突触后与突触前脉冲时间差$s=t_j^f-t_i^f$在学习窗口内。
      • 当$s\ge0$时，$a_2^{post,pre}(s)>0$，则如果突触后脉冲$t_j^f$在突触前脉冲的到达时间$t_i^f$之后的较短时间内发放，在$t_j^f$时刻，突触权值的改变量为$a_1^{post}+a_2^{post,pre}(s)>0$
      • 当$s<0$时，$a_2^{post,pre}(-s)<0$，则在$t_i^f$时刻，突触权值的改变量为$a_1^{post}+a_2^{post,pre}(-s)<0$

基于局部变量的stdp实现

  1. 基于脉冲对的STDP规则

    待更新

  1. 基于三脉冲的STDP规则