从之前的学习可以了解到,并不是复杂的模型就可以得到更好的训练结果。复杂的模型可能造成过拟合(overfitting)的情况。简单来讲,以线性回归为例,就是在过于贴合训练集上每一个数据点,导致曲线过于“崎岖”,而在测试集上的表现并没有更好,loss 变的更大了。
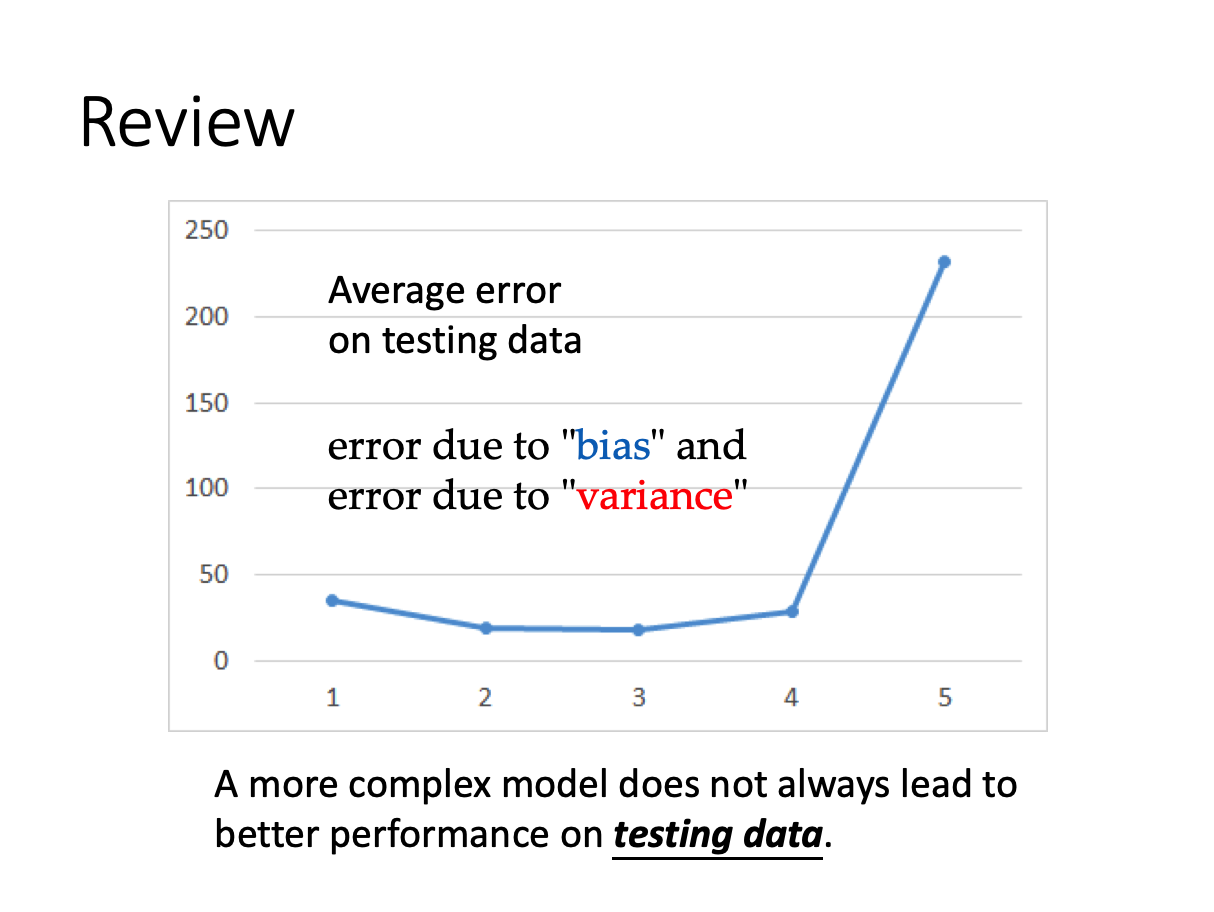
训练结果的错误来自于两方面:偏差bias和方差variance
假设变量x的期望为 μ
m为不同训练结果得到的x均值
很显然$m=\frac{1}{N}\sum_{n}x^n\neqμ$
……
同理变量实际x和均值m做差得到的方差$s^2$不等于方差的期望$σ^2$
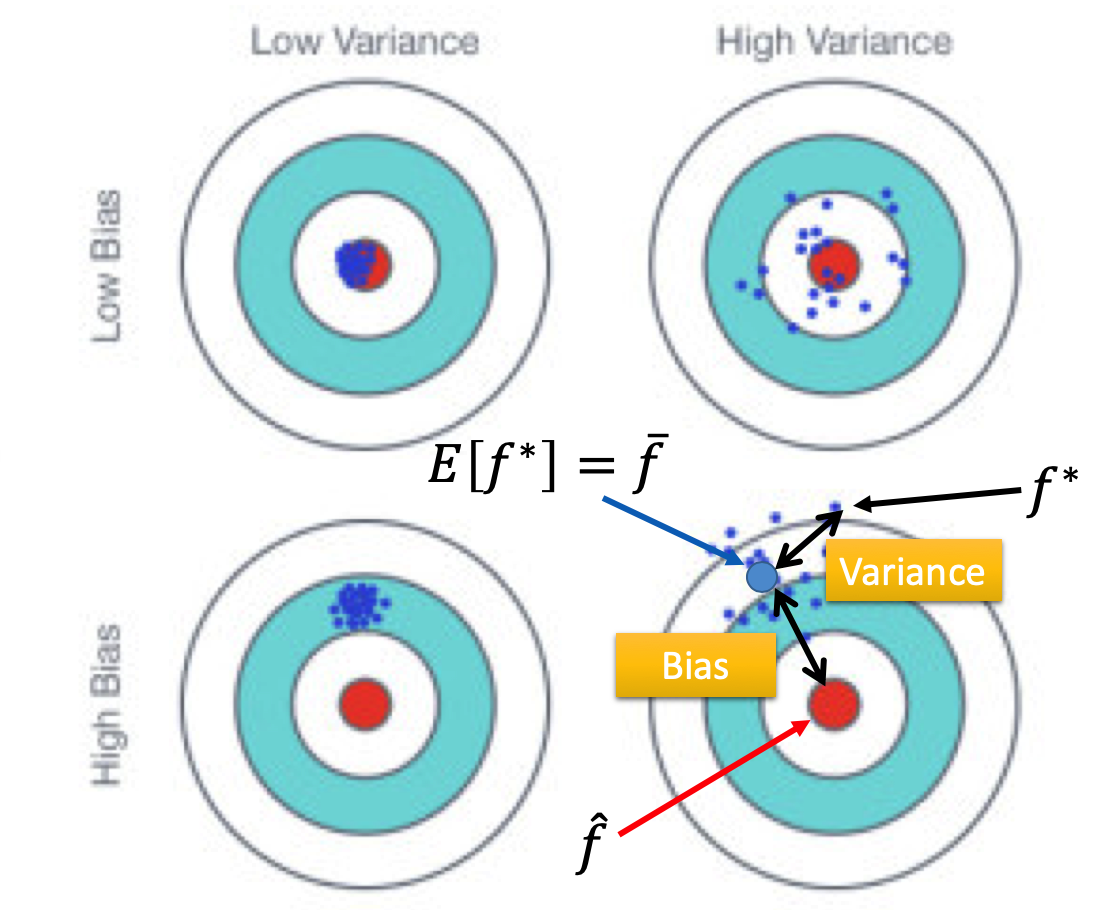
如下图可以看出bias和variance错误之间的差别以及对训练结果的影响。
其中$f^*$为不同训练集下,训练得到的合适的function
$\overline{f}$为$f^*$的期望,即得到的所有合适的function的平均
右上角的靶子可以看出,方差比较大的$f^*$比较分散,但是他们的均值m距离正确结果很近。
而左下角的靶子显示,bias比较大的$f^*$比较集中,但是他们的均值距离正确结果很远。
右下角的靶子表明,靶心和$\overline{f}$之间的偏差是由于bias导致的,而每一个单独的$f^*$与$\overline{f}$的偏差是由于variance